Magnus Harder

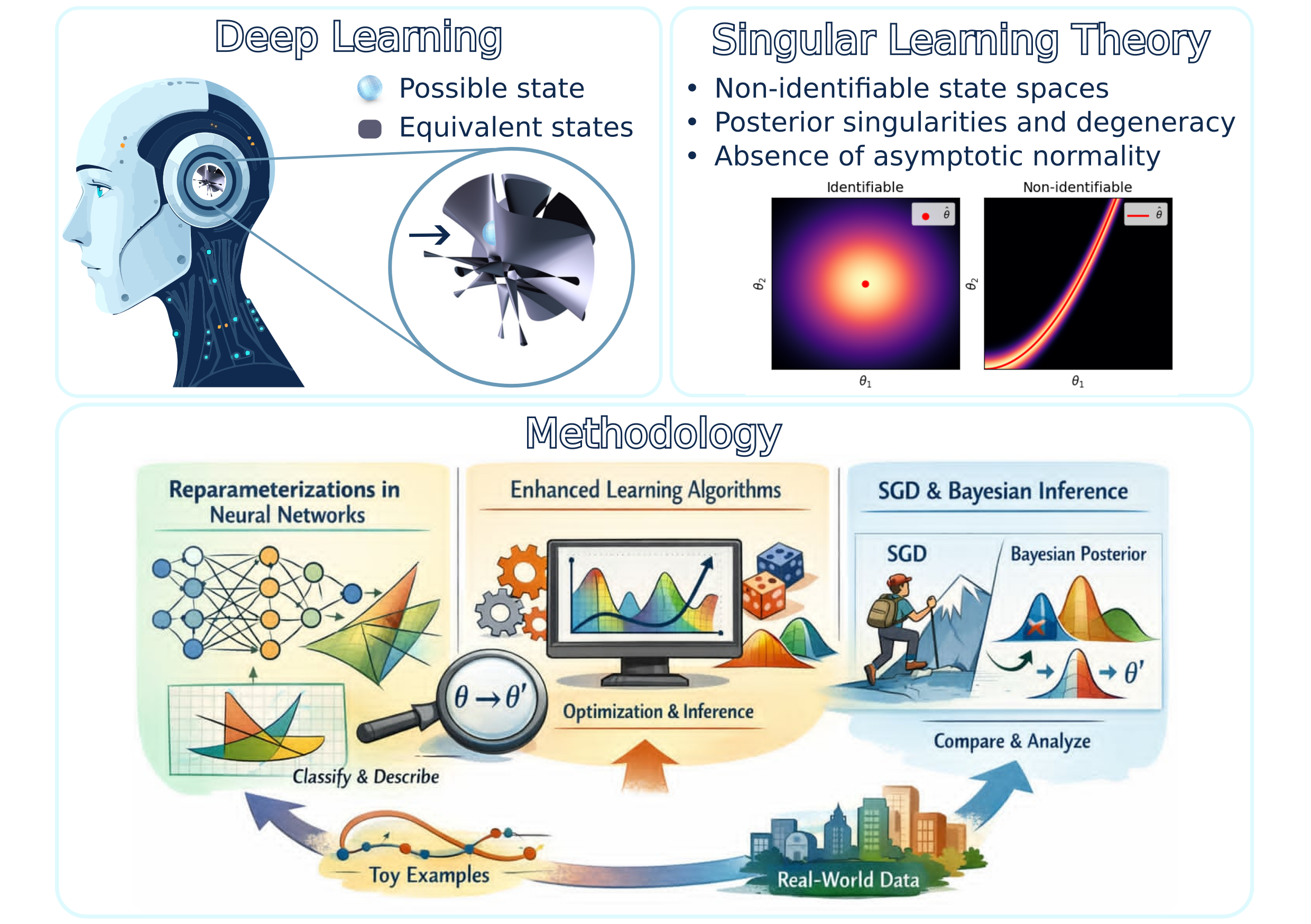
AI has made significant progress in recent years, supporting decision-making across many domains. Since AI predictions are inevitably fallible in some situations, providing reliable measures of uncertainty is essential for building trust. This project focuses on Bayesian deep learning, a type of AI that not only makes predictions but also quantifies its own uncertainty, helping to identify when an AI knows something, and when it might be wrong.

Many of today’s AI systems remain limited in a crucial respect: they often make accurate predictions but provide no measure of uncertainty or unreliable ones. Current Bayesian deep learning methods often fail, largely because existing Bayesian approximations are too unreliable. Recent work, however, shows that accounting for hidden structural properties of neural networks can lead to significantly more reliable uncertainty estimates.

This project combines algebraic geometry (mathematics) and singular learning theory (statistics) to study how Bayesian neural networks learn. Using these frameworks, we will develop the theory needed to design fast algorithms that account for the hidden structural properties, ultimately leading to more reliable Bayesian approximations and thus improved uncertainty quantification.

‍